Table of Contents
Determine Grain Sizes
The TIMEleSS tools contain two scripts to determine the volume of each grain in the sample. These are timelessExtractGrainSizes.py to obtain relative grain volume and timelessRelToAbsGrainSize.py to convert these relative grain sizes into absolute values. The scripts provide both a list of the grain volumes and a simple histogram of the grain size distribution.
Method
The idea behind the scripts is to compare the theoretical peak intensity with the actual peak intensity from the experiment. This comparison gives a size value for each grain, which is proportional to the volume of the grain. As a result, the script provides a list of those relative grain volumes.
In a second step, the sum of this list of relative grain volumes is put in relation to the illuminated volume of the sample chamber. The result of this second step is a factor, which tells you, how many units of relative grain volume represent 1 µm^3. This is then used to re-write the list of relative grain volumes to a list of absolute grain volumes.
Usage
To use the scripts, the process of indexing must be finished already, i.e. a GrainSpotter output file is required. Then, execute the two scripts sequentially.
1. Extract relative grain sizes
Try this:
timelessGrainSizes.py -o myoutputfile.txt -w 0.3738 -HV True mylogfile.log peaks-t100.flt crystal.cif
This command should do the following:
- Display a number of rejected grains in the command window
- Display the relative grain volumes in the command window
- Save the list of grain volumes into the file myoutputfile.txt and
- Plot a simple histogram of the grain volumes
Help message:
Estimation of relative grain volumes based on diffraction intensities
Example:
timelessGrainSizes.py -w 0.3738 mylogfile.log peaks-t100.flt crystal.cif
This is part of the TIMEleSS project
http://timeless.texture.rocks
positional arguments:
logfile Path and name for GrainSpotter output file
fltfile Path and name for fltfile
ciffile Path and name for CIF file
optional arguments:
-h, --help show this help message and exit
-w WAVELENGTH, --wavelength WAVELENGTH
Wavelength (angstrom, required)
-m TTHETA_MIN, --ttheta_min TTHETA_MIN
If set, minimum 2 theta for calculation of peaks from cif file (degrees). Guessed from GS output file otherwise.
-M TTHETA_MAX, --ttheta_max TTHETA_MAX
If set, maxium 2 theta for calculation of peaks from cif file (degrees). Guessed from GS output file otherwise.
-o OUTPUT, --output OUTPUT
If set, saves result to this file. Default is None (no filter)
-HV HISTOGRAM_VOL, --histogram_vol HISTOGRAM_VOL
If set, plots a histogram of the grain volumes on the screen. Default is False
-HR HISTOGRAM_RAD, --histogram_rad HISTOGRAM_RAD
If set, plots a histogram of the grain radii on the screen. Default is False
-b HISTOGRAM_BINS, --histogram_bins HISTOGRAM_BINS
Sets the number of histrogram bins. Only works if histogram is set True. Default is 60
-r REJECT, --reject REJECT
Reject grains with AverageI > reject*MedianI. Default is 20.0
Rejected grains
Since the script is based on the analysis of the peak intensities, it also detects outliers in a grain, e.g. if one of the peaks is significantly more intense than the others. If this mismatch is above a certain threshold, the grain is rejected by the script. You can adjust the threshold by adding the parameter -r when executing the script (see help message above).
List of relative grain volumes
The command line will show a list of relative grain volumes. If you set the histogram option -HR to True, you can force the script to calculate grain radii instead of grain volumes (This goes not only for the histogram but also for the list of grain sizes itself.) If you chose the option -o, it will save this list in a file. Note that this output file is necessary if you want to convert the relative grain sizes to absolute ones later.
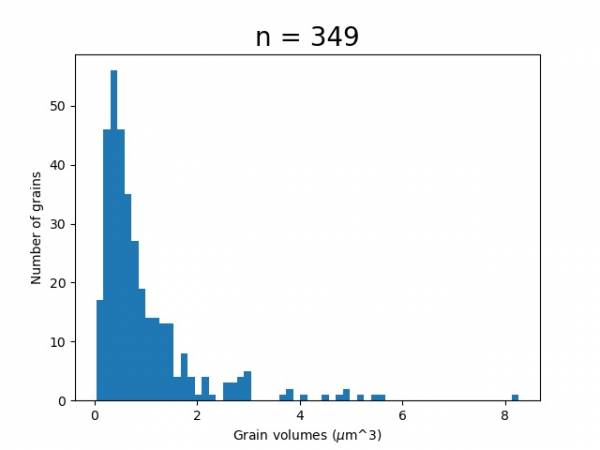
Histogram
2. Convert to absolute grain sizes
Try this:
timelessRelToAbsGrainSize.py myoutputfile.txt -H 1.5 -V 1.8 -r 56 -t 20 -i 76.2 -hist 60 -prop 0.85
This command will:
- Read the output file of
timelessGrainSizes.py - Convert the relative grain volumes into absolute grain volumes (in µm)
- Save the absolute grain volumes in a new file
myoutputfile_abs.txtand - Plot a histogram similar to the one shown above
The explanation of the individual parameters is given in the help:
# Explanation of the parameters: grainsizelist: An output file from the "timelessExtractGrainSizes.py" script. Should be a regular text document -H & -V # beamsize_H and beamsize_V: Horizontal and vertical dimension of the X-ray beam in $\mu$m. Necessary to calculate the illuminated sample volume. -r # rotationrange: Full rotation range used in the experiment in micrometer. Necessary to calculate the illuminated sample volume more accurately. -t # samplethickness: Thickness of the sample in micrometer. Necessary to calculate the illuminated sample volume. -i # indexquality: Quality of the previous indexing process in percent. Used to account for the fact that not all grains were found during the indexing. -rad # radius: Boolean operator that determines if grainsizelist consists of grain volumes or grain radii. True means volumes, False means radii. -hist # histogram_bins: Number of histogram bins you want to use. By default, no histogram is plotted. -prop # proportion: Defines how much of the sample is your phase of interest. Can be between 0 and 1.
Estimation of the illuminated volume
The entire conversion is based on the correct estimation of the volume that is illuminated by the X-rays. Normally, this would be a simple cuboid:
V = a * b * c
where a, b and c are the gasket thickness and the dimensions of the X-ray beam.
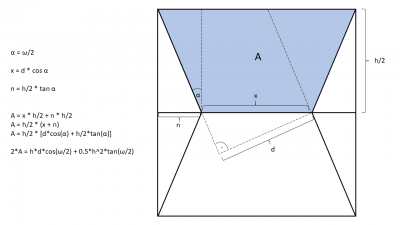
However, because the sample is rotated, the actual volume is larger: The actual illuminated volume of a rotated sample chamber is:
V_r = v * [d * h * cos(ω/2) + 0.5 * h^2 * tan(ω/2)]
with
- v = beamsize parallel to the rotation axis (usually vertical)
- d = beamsize orthogonal to the rotation axis (usually horizontal)
- h = gasket thickness
For a graphical explanation, see the following sketch:
A quick calculation example shows the difference:
v = 2 µm d = 2 µm h = 20 µm ω = 56° V = 80 µm^3 V_r = 283 µm^3
The example shows that the volume, which is illuminated by the X-rays, can increase drastically when the sample is rotated. Therefore, the accurate estimation of the illuminated volume is crucial for the determination of the precise conversion factor.
Error estimation
While the dimensions of the X-ray beam and the rotation angle are usually well known, the thickness of the gasket in a diamond-anvil cell experiment is less constrained. This is due to the fact that the initial indentation thickness is getting thinner as the pressure is increased during the experiment. Usually, the rate, at which this happens, is unknown. Measuring the actual gasket thickness after the experiment can help to model the thickness evolution throughout the experiment. This can, however, still only be an approximation of the true thickness.